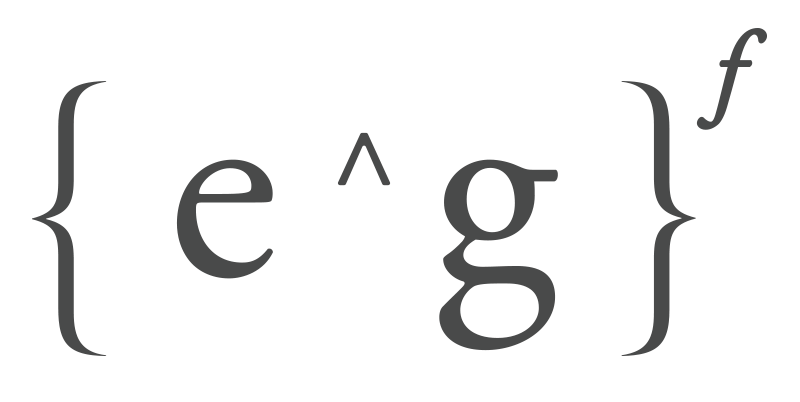Math Function Based Animations and Behaviors for UI Animations

 

Today, the world of UI Design is full of beautiful layouts and animations that are not only aesthetically pleasing, but also compelling. The richness of these UI's relay solid principles of traditional animation: Squash and Stretch, Anticipation, Secondary Animation, Timing, Exaggeration, Arc, Slow In, Slow Out, etc. I believe adding these nuances to the animation make a higher connection with the user on a deeper level. Humans as organic beings lack almost any linear or constant behaviors in their motion. Having angular articulations, we form beautiful arcs and lines in our everyday movements and use constant acceleration/deceleration in our movements, for example, to aid communication in the case of our hands, with sharp and precise turns, stops and points when emphasizing a point, all the way to the gentle swing of when moving them to a melody or giving a simple wave. These variations in time and speed are crucial to the richness of the communication process, and thus a higher level of engagement with the user.

Figure 1a.- The animation shows a linear interpolation, notice that the base ring intended lacks of protagonism and might even go unnoticed in a VR or AR situation.

Figure 1a.- The animation shows a linear interpolation, notice that the base ring intended lacks of protagonism and might even go unnoticed in a VR or AR situation.

Figure 1b.- The animation shows the smoothstep interpolation giving the highlighting of the object emphasis acompanied by some elegance due to acceleration and deceleration.

Figure 1b.- The animation shows the smoothstep interpolation giving the highlighting of the object emphasis acompanied by some elegance due to acceleration and deceleration.

Figure 1c.- The animation shows a modified smoothstep function, notice how the modification of the function gives a more urgent connotation to the highlighting of our object.

Figure 1c.- The animation shows a modified smoothstep function, notice how the modification of the function gives a more urgent connotation to the highlighting of our object.

In this study we will mathematically deconstruct one of the most used principles in today's UI design and animation, "Slow In and Slow Out." We will be able to also learn to modify while understanding its translation as an expression in the MEL (Maya Embedded Language), and how to take this fundamental understanding and examine the different variations to be applied, not just to a piece of our animation, but to actually be able to develop a language that can be represented by a formula or expression that can be deployed or scripted, and then tied to the guideline of our design and experience, from prototypes and early explorations, to personal and professional projects.

In and Out

Slow In and Slow Out can be represented graphically by a smooth interpolation function from 0 to 1 where, in contrast with the linear interpolation in the value from 0 to 1 (Figure 1a), one can notice animation stages as acceleration, momentum, peak, and deceleration, all before the final stop of the graphical form.

 
Figure 2a.- Notice that the linear interpolation maintains a constant speed and does not provide any extra other than the information of the translation of the object

Figure 2a.- Notice that the linear interpolation maintains a constant speed and does not provide any extra other than the information of the translation of the object

Figure 2b.- The Smoothstep interpolation adds a richer and more natural behavior to the translation of the object from point A to B

Figure 2b.- The Smoothstep interpolation adds a richer and more natural behavior to the translation of the object from point A to B

 

SYNTAX AND APPLICATION

The smoothstep function syntax for the two cases that we will touch in this study (MEL expresions and Unity)  are the following

For MEL ( smoothstep ) :

float smoothstep(float start, float end, float parameter)

For Unity ( Mathf.SmoothStep ) :

public static float SmoothStep(float from, float to, float t);

To get the same result as figure 2b we can start with the same pseudo code:

Purple_circle.translateY = smoothstep (0,1,time);

This pseudo code would make our circle move starting at 0 time ( our start float ) to 1 ( our float unit ) using our unit of time (24fps, 29.97fps, 60fps, etc). This range will always be confined to a 0 to 1 range, a range which can be modified and will be explored in this study.

PLAYTIME

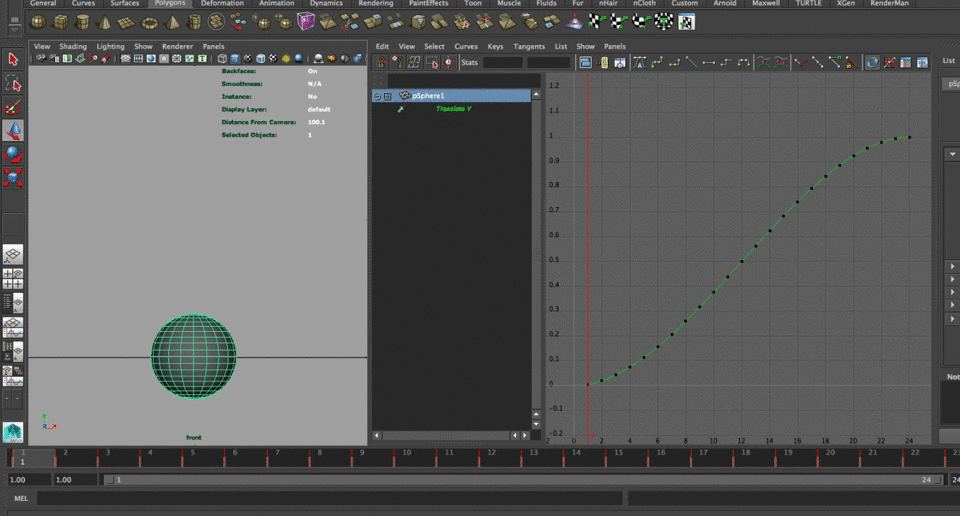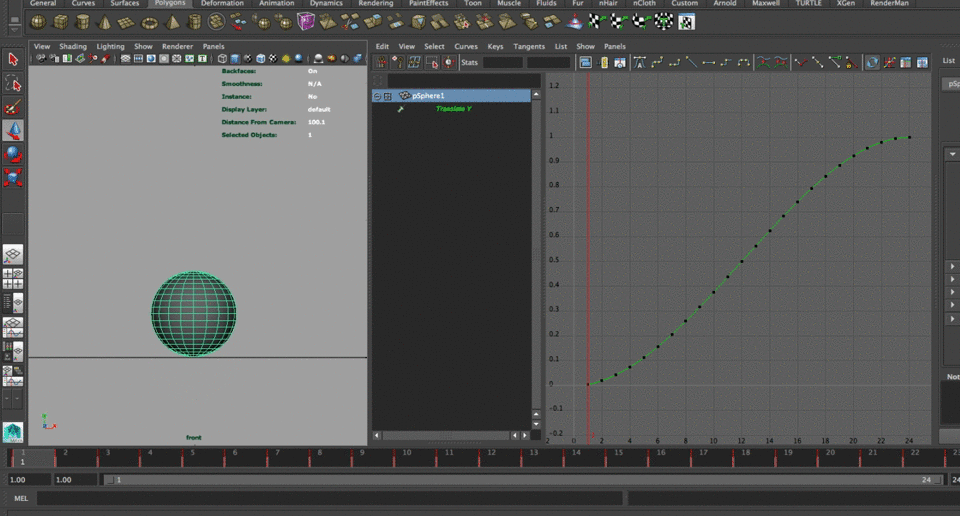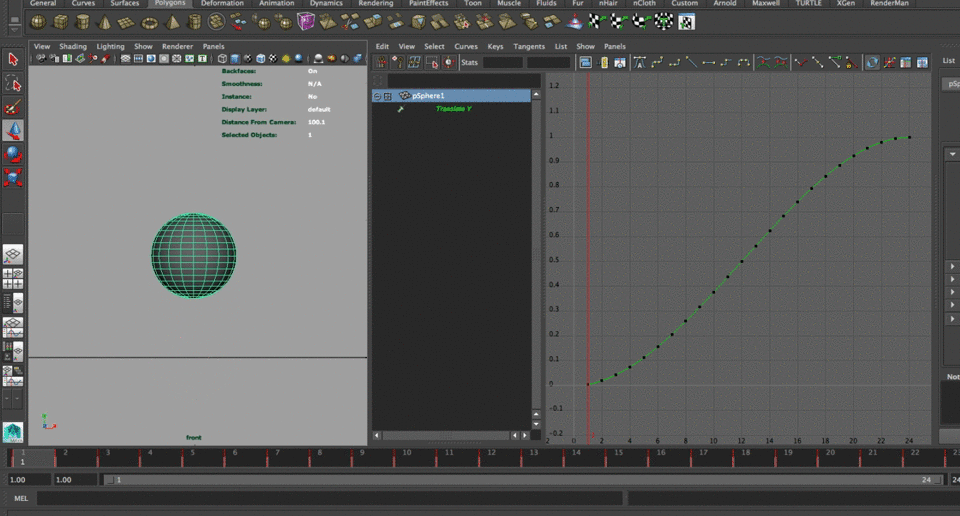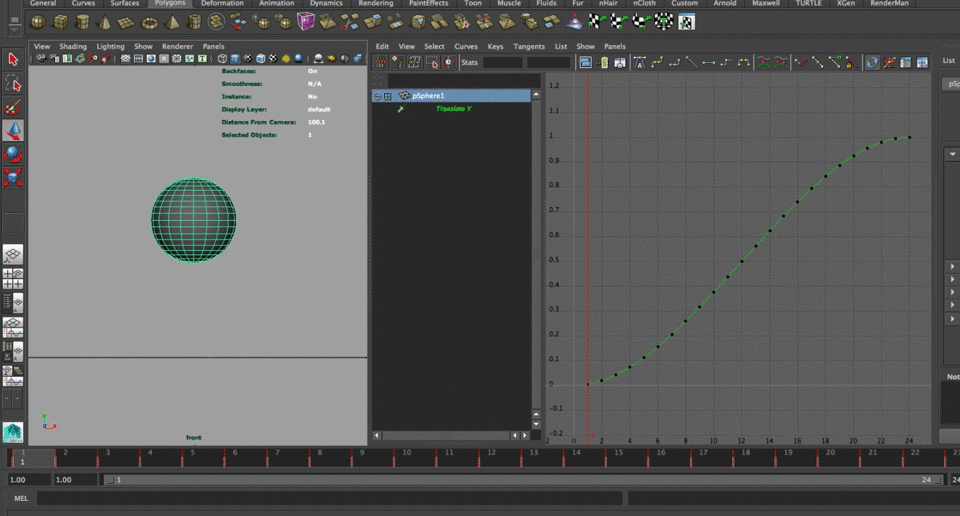
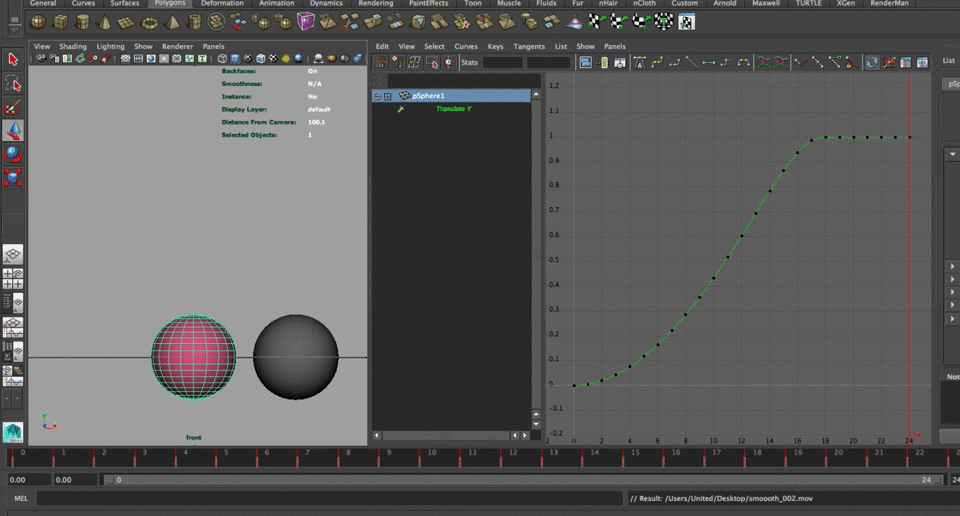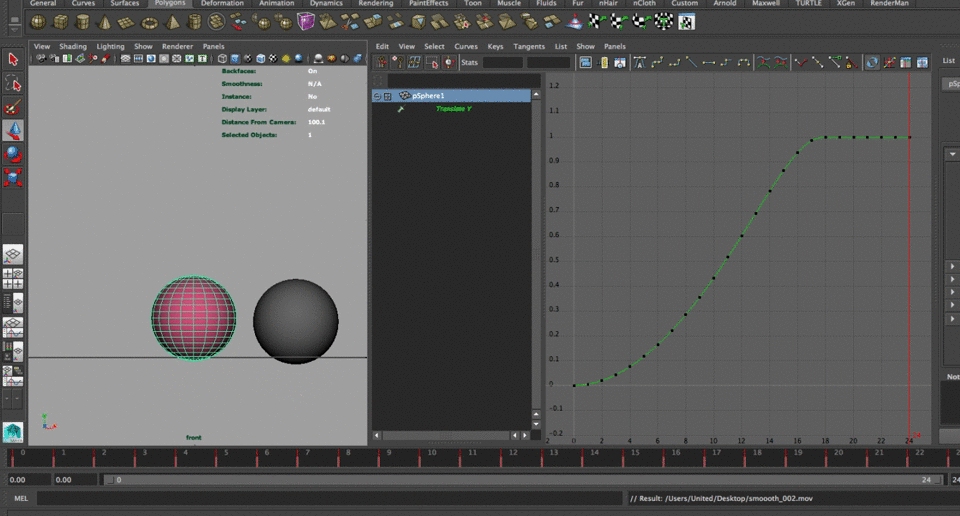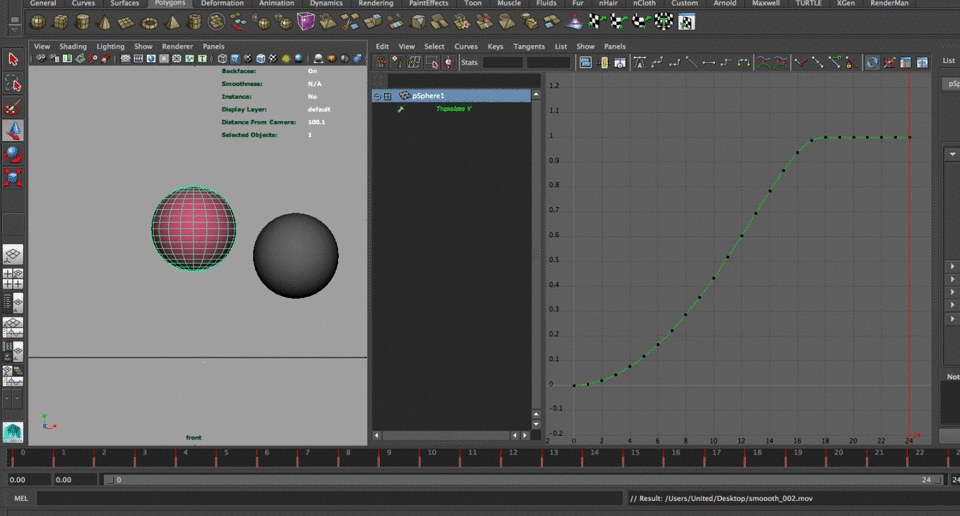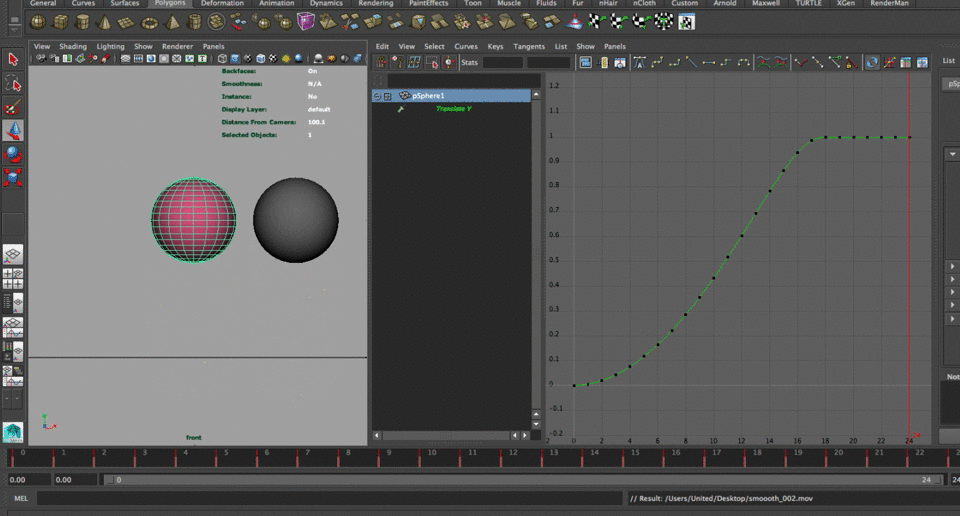
To have a more accurate description and examination of what the code does, we will work in parallel with Maya and look at the output of the curves since the initial basic syntax all the way to the modifications that we will apply to the function. We created a polygonal sphere. I called it pSphere1 and I applied the simple smoothstep function to modify its Y translation

pSphere1.translateY = smoothstep(0,1,time);

That, as you guessed, gave us the following animation curve (in Maya you're not able to look at curves when an expression is connected, so I ran a quick editable bake key frames script that I find really useful when modifying expressions while still getting visual feedback)

 

We can now start modifying the curve based on the line:

pSphere1.translateY = smoothstep(0,1,time);

I will create a variable that will start on the initial number (1 in this case, I also used cosine since it starts evaluating at 1) to replace the second float and therefore add a steeper curve towards the end:

$mod = cos(time); pSphere1.translateY = smoothstep(0,$mod,time);
 

As you can see on the curver we have altered the number but we have also shorten the time of animation (which we will solve shortly)

now lets try something with a little more character...

$mod = cos(time*2.5); pSphere1.translateY = smoothstep(0,$mod,time);
 

Notice that we have gained a different kind of behavior in our object in comparison with the original, but we have shortened the time of action to about half. We will solve that adding a variable to our modifier.

$mod = cos(time * 1.5); $mod_ret = $mod * 4; pSphere1.translateY = smoothstep(0,$mod_ret,time);
 

Secondary animation, such as a bounce before hitting the final resting position can also be achieved by combing functions, except this time we use the core of the smoothstep function to drive the curve, in this instance affected by a sin function, as shown on the following lines:

$dim = smoothstep(0,1,time); pSphere1.translateY = sin($dim*2)*1.5;
 

SUMMARY

The functions and behaviors generated in this study can be because of the type of data they output (float) applied across many of the properties of a UI element, such as scale (homogeneously or in each axis individually), translation, rotation, and many other inputs like shader properties, opacity, glow, etc.

The main purpose of this study is to serve as somewhat of a catalyst to help artists and studios making experiences that involve motion and animation to be able t o establish more faithful motion design guidelines for more solidly designed experiences and products. A good analogy, as to not think of this as a disregard for the beauty of any animation done by the artist, would be to think of these methods as the transformation of a logo from beautiful hand-traced lines into vector art, a transition made to be able to create the language and guidelines for the motion behaviors and animations surrounding their experiences.

 

Thank you for your time!